快速理解超前进位加法器
写在前面
为了方便理解,本文会出现算式,但难度约等于1+1=2。详细推导请移步参考文献👍
2'bxxx表示:2位宽的2进制数xxx
最简单的加法器😎
最简单的加法器即半加器,他的输入输出可表示如下
A+B=2'bS
例如:1+1=2'b10
两个半加器组合形成全加器,即将第一个半加器的进位输出,给到第二个半加器的输入,他的输入输出可表示如下
A+B+C =2'bS
例如: 1+1+1=2'b11
串行加法器 RCA🚲
恭喜,你现在可以实现一个64位的串行加法器了👍什么,你说你不会🤔别急,让我们从竖式加法开始~
1 1
+ 1 1
1 1 0
聪明的你一定发现了,在十位计算中使用了进位,这也是全加器的来源。那么,如果将这个式子一直往左扩大到64位,使用64个全加器计算本位与进位不就能得到一个串行加法器了吗?答案是肯定的。
可惜,这种加法器有一个致命缺陷,如果你有一定的数电基础就能敏锐发现。如果没有,可以这样通俗的理解:“一个电路从输入改变到输出改变需要一定时间,也称作延迟。在串行加法器中从第二位(十位)开始,就需要进位输入参与运算,同时得到下一个进位输出。第三位(百位)亦是如此,但它的进位输入需要等待第二位(十位)的进位输出,也就是他需要等待3个半加器的延迟,以此类推64位串行加法器需要等待2*63-1个半加器的延迟,这是不可接受的✋
超前进位加法器 CLA🏍
如何解决这个该死的延迟!标准回答:以时间换空间。使用更多的硬件资源并行计算进位。
将每一个进位展开化简可以得到超前进位加法器,以下是四位宽CLA实现公式(图片来自互联网优秀资源,公式推导可以太长不看,延迟对比有个印象就行):

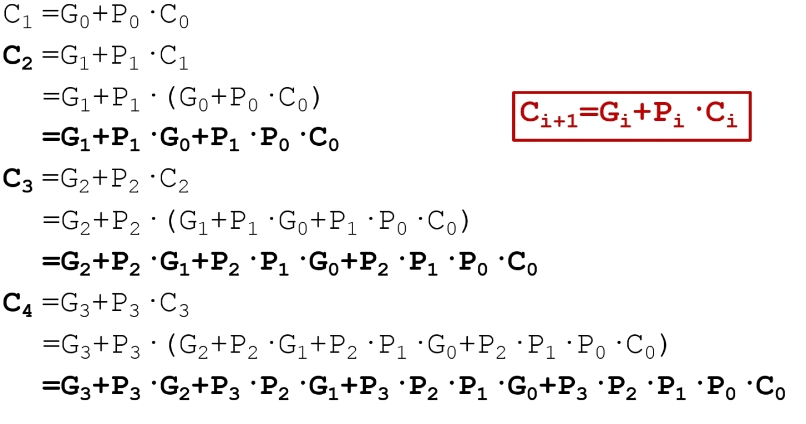
CLA与RCA延迟比较:
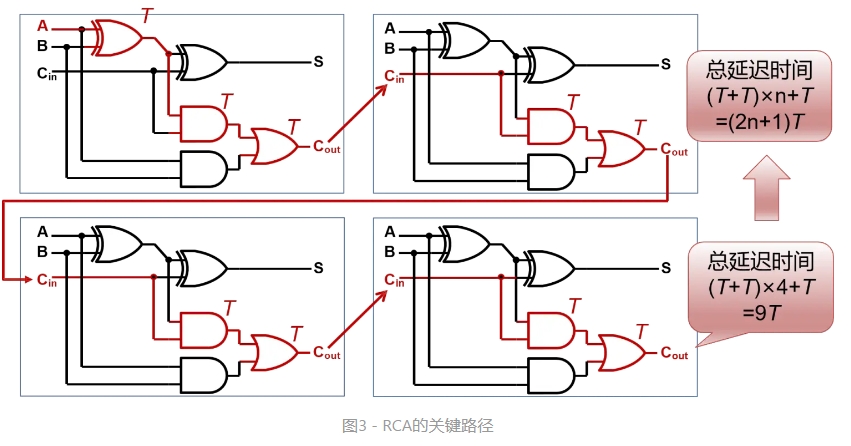
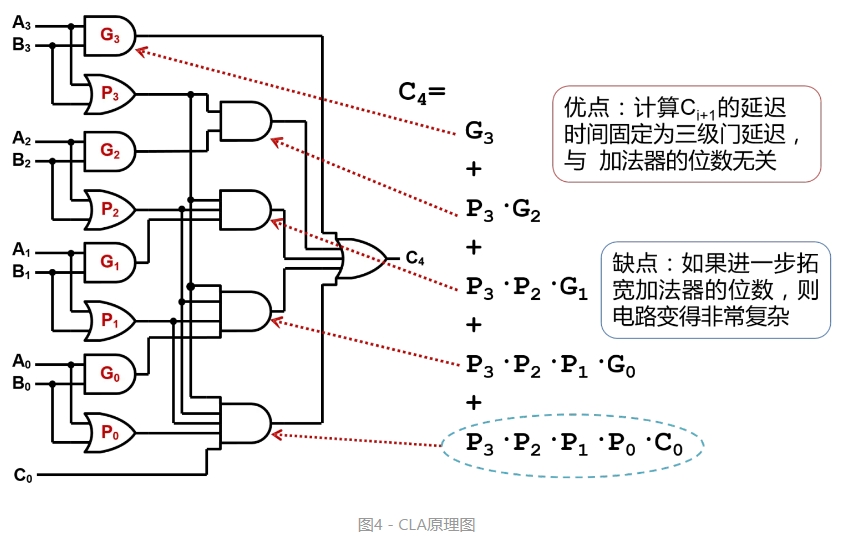
可以看出消耗的资源按指数级上升,不可能将64位全部展开。当然,我们可以重复使用超前进位,实现多级超前进位加法器,胜利就在眼前!
多级超前进位加法器
如果你对上文的超前进位加法器理解不是很透彻,没关系接下来你只需要知道几个重点:
- 超前进位加法器可以直接输出各级进位
- 将进位与本位相加后可以直接得到输出
- 位数越高消耗资源越夸张,一般取CLA4
CLA电路如图所示:
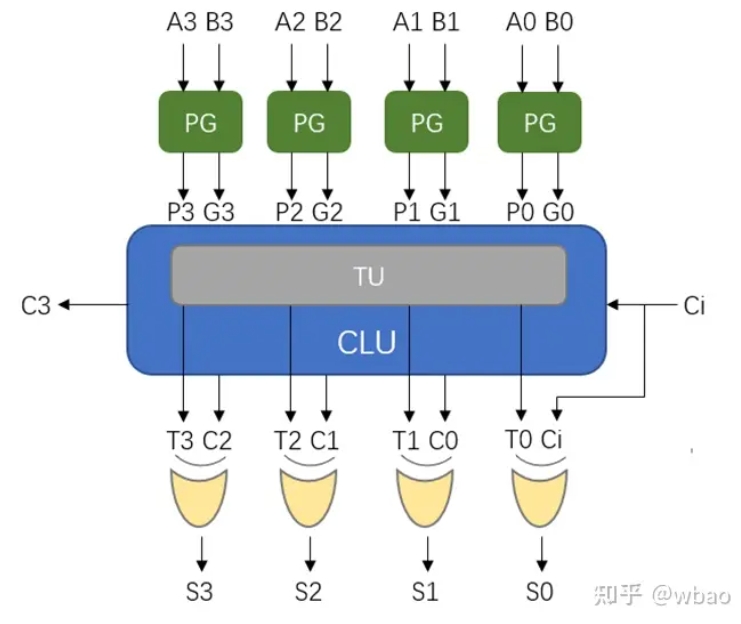
如果将CLA的进位串行连接,进位的延迟就会阴魂不散,神奇的是我们可以再次使用超前进位!
将进位分解为PG形式,单独拉出来并接入一个新的CLA模块,就可以并行计算多个CLA模块的进位,如下图所示(C7和C3反了):
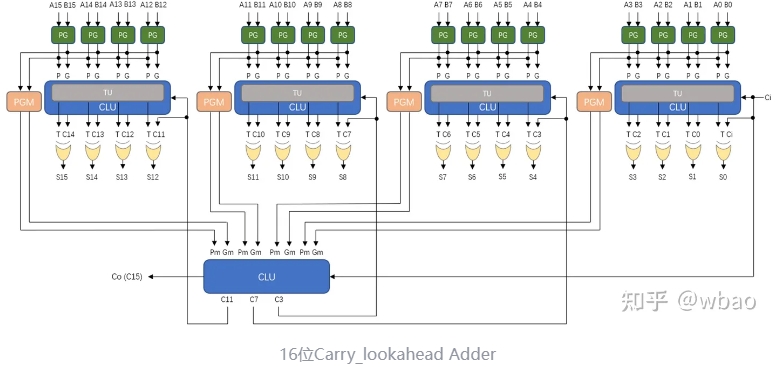
有几个需要注意的点:
- 二级CLA需要接入来自最初始的Ci(如果存在)
- 同级CLA的Ci输入来自高级CLA的Co
总结
到这里我相信你已经理解了超前进位加法器,虽然我认为公式推导也是相当重要的一部分,但理解才是设计电路的基础。没想到加法器这么简单😒,写的时候脑子里一直想着压缩器导致有点啰嗦,下一篇就写乘法器😉
如果这篇文章能帮到你是我的荣幸,感谢。
参考文献
306 - 加法器的优化——超前进位加法器(Carry-Lookahead Adder,CLA) - 简书 (jianshu.com)