快速理解Booth乘法器
串行乘法器
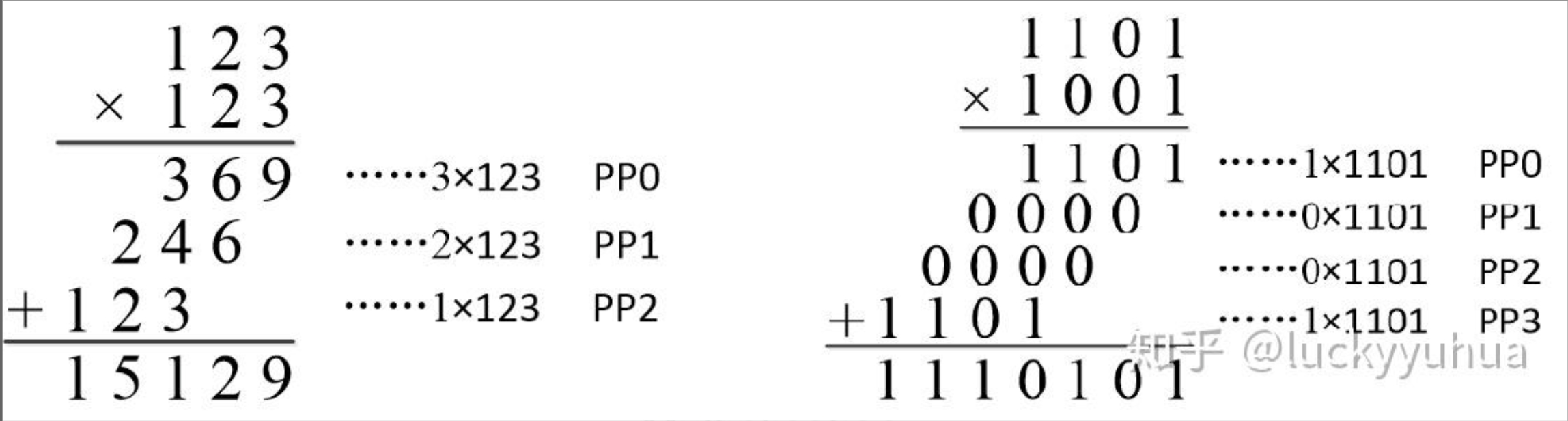
回忆竖式乘法,首先每一位与另一个数相乘,再将所得的积全部相加。在二进制中,相乘结果甚至只有它本身和0! 也就是只需要一个选择器和一个加法器就能实现串行乘法器,代价是很长的计算周期。
Booth编码
核心思想:乘法计算中如果出现0则他的部分积为0,如上图右侧PP1、PP2,Booth变换能增多0的个数(具体实现请参考附录),但不能减少部分积的个数,在并行硬件电路设计中还是需要相当数量的加法器。改进booth编码能减少部分积个数,基4booth编码能减少一半部分积个数,如图:
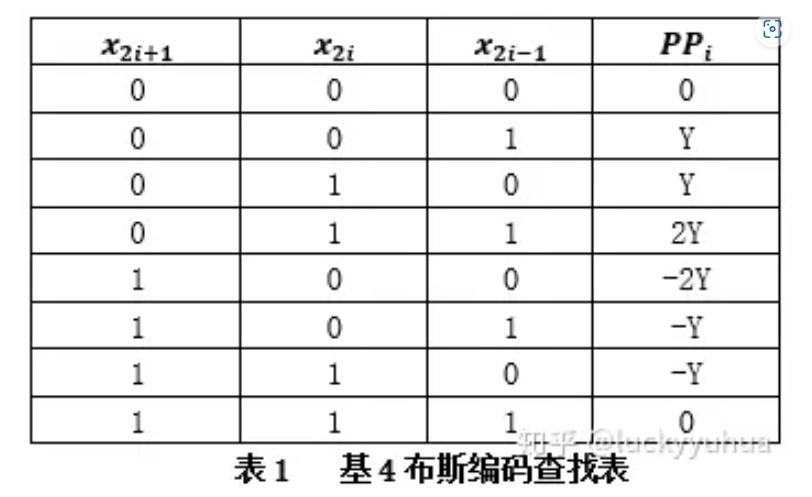
5-3压缩器(4-2压缩器)
除了减少部分积个数,累加器延迟也是影响计算速度的重点,如图注意红色部分延迟:
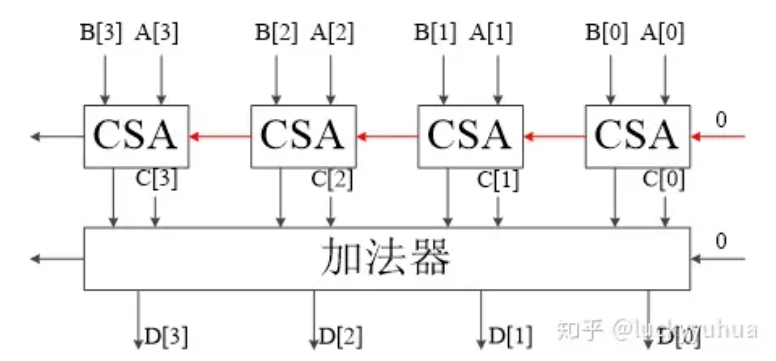
加以改进就能实现一个3-2压缩器,如图
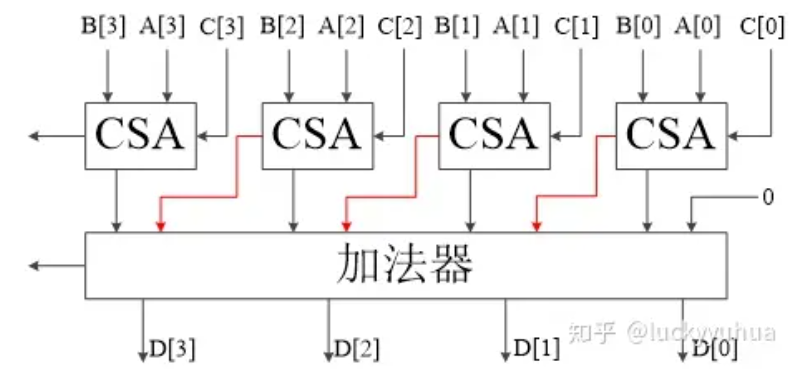
可以同时计算三个加数输出两个加数,还有一中压缩率更高的5-3压缩器具体实现参考附录。
最后
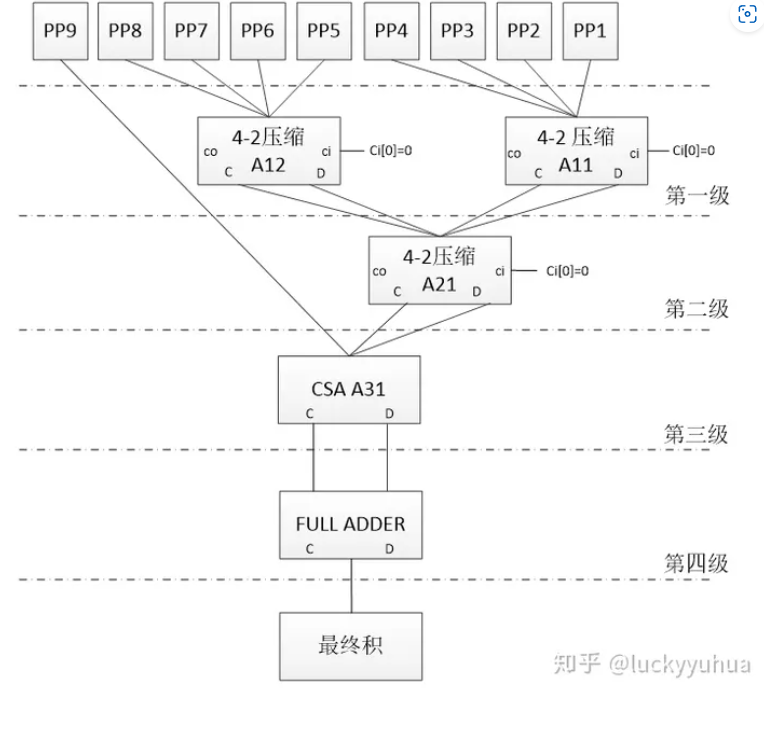
将所有部分积压缩成两个加数,使用加法器相加就实现了一个Booth加法器。